"Su teoría es disparatada, pero no lo suficientemente disparatada para ser verdad."
Niels Bohr
En los tres post anteriores de este monográfico de mecánica cuántica vimos la dualidad onda-partícula, la cuantización de la energía, el principio de incertidumbre y el colapso de la función de onda. Ahora trataremos sobre cuando tenemos que aplicar la mecánica cuántica y cuando la clásica, veremos el principio de exclusión y sus consecuencias, y la misteriosa propiedad de "no localidad" que presenta el mundo cuántico. Con todo este material podremos discutir las profundas implicaciones que tiene la teoría cuántica en la comprensión de la realidad física.
El mundo clásico como límite del cuántico
De lo dicho hasta ahora, ondas de probabilidad, cuantización, principio de incertidumbre, parece seguirse que el mundo de lo muy pequeño sigue unas leyes diferentes de nuestro mundo habitual, pero no es así. De la misma forma que la teoría de la relatividad tiene efectos despreciables a velocidades muy inferiores a la de la luz, pero va cobrando importancia cuando consideramos velocidades mayores, también ocurre lo mismo con la mecánica cuántica, que tendrá efectos progresivamente más importantes a medida que los objetos que consideramos se reducen en masa y tamaño.
Por ejemplo, consideremos el principio de incertidumbre de Heisenberg que mencionamos en la parte III, que como decíamos prohíbe el conocimiento simultáneo de ciertos pares de magnitudes, como la posición y la velocidad. Matemáticamente podemos expresarlo en la forma
donde x es la posición, p es la cantidad de movimiento (que es igual al producto de la masa m por la velocidad v) y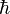 
es la constante de Planck h dividida por 2π, que en el sistema internacional de unidades tiene un valor de 6,6·10⁻³⁴ J·s . Observemos que la fórmula relaciona las incertidumbres de las magnitudes, de ahí los símbolos en forma de triángulo Δ. La constante h tiene un valor realmente pequeño: pensemos en un grano de arena fina, de diámetro 0,06 mm y 0,67 mg de peso, y con una indeterminación (error de medición) del 1%; con estos valores la fórmula nos dice que la indeterminación en la velocidad del grano de arena es de 7·10⁻²³ metros por segundo, o sea 0,00000000000000000000007 m/s, un error absolutamente despreciable. Dicho de otro modo, podemos determinar la velocidad del grano de arena con una precisión prácticamente del 100% (del 99,99999999999999999999993%). También podemos visualizar lo pequeño de este error en la determinación de la velocidad pensando que un objeto que se moviese a 7·10⁻²³ m/s tardaría en avanzar un milímetro... ¡unos 5.000 millones de años!
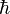es la constante de Planck h dividida por 2π, que en el sistema internacional de unidades tiene un valor de 6,6·10⁻³⁴ J·s . Observemos que la fórmula relaciona las incertidumbres de las magnitudes, de ahí los símbolos en forma de triángulo Δ. La constante h tiene un valor realmente pequeño: pensemos en un grano de arena fina, de diámetro 0,06 mm y 0,67 mg de peso, y con una indeterminación (error de medición) del 1%; con estos valores la fórmula nos dice que la indeterminación en la velocidad del grano de arena es de 7·10⁻²³ metros por segundo, o sea 0,00000000000000000000007 m/s, un error absolutamente despreciable. Dicho de otro modo, podemos determinar la velocidad del grano de arena con una precisión prácticamente del 100% (del 99,99999999999999999999993%). También podemos visualizar lo pequeño de este error en la determinación de la velocidad pensando que un objeto que se moviese a 7·10⁻²³ m/s tardaría en avanzar un milímetro... ¡unos 5.000 millones de años!
Por otra parte si consideramos un electrón, moviéndose en una órbita de diámetro de dimensiones 10⁻⁸ cm, con una masa 9·10⁻²⁸ gramos, nos resulta una incertidumbre en la velocidad de unos 10⁶ metros por segundo, esto es ¡1000 kilómetros por segundo! Dicho de otra manera: si determinamos la posición no podemos tener ni idea de la velocidad del electrón.
Paquetes de ondas, estados cuánticos puros y compuestos
La relación de incertidumbre puede expresarse gráficamente imaginando que una partícula cuántica es una superposición de ondas tal que produce un paquete de ondas, una onda que tiene amplitud distinta de cero solo en cierta región pequeña del espacio; esta región se mueve con el tiempo, y podemos imaginar que se corresponde con la posición de la partícula, de hecho la partícula es el paquete de ondas. La indeterminación en la posición se corresponde con la anchura del paquete. En la figura la línea de puntos roja delimita la envolvente del paquete, que se desplaza por el espacio con la denominada velocidad de grupo del paquete.
Matemáticamente los paquetes de onda se forman por superposición de ondas distintas que interfieren entre sí. Físicamente se denominan estados puros a las ondas componentes que al combinarse forman los estados compuestos, representados por paquetes de ondas. Cada estado puro tiene asociada una función de onda cuántica, y el estado compuesto es la suma de funciones de onda.
Hay una relación entre estos estados y el proceso de medición: si en un sistema en estado puro se efectúa una medición, el sistema pasa a estar en un estado compuesto: la medición destruye el estado puro. Por ejemplo un electrón libre, antes de efectuar mediciones, está en un estado puro, con una función de onda "simple" que se extiende por todo el espacio; en el momento de medirlo le forzamos a comportarse como partícula, con lo cual se convierte en un paquete de ondas localizado que es una mezcla de estados puros.
donde φ es la función de onda de la partícula, relacionada con la probabilidad de encontrarla en una cierta posición, H es el operador de Hamilton, relacionado con la energía de la partícula, y dφ/dt es la variación de φ con el tiempo. Con un poco de matemáticas que no detallaremos, esta ecuación se transforma en
El principio de exclusión fue descubierto por Pauli en 1925, resolviendo muchos problemas técnicos importantes de la época como por ejemplo los detalles de la estructura atómica o de la valencia química. Pauli descubrió el principio en relación a los electrones, enunciando que no más de dos electrones de un átomo no pueden tener el mismo estado de movimiento. Este “estado” se definía en esa época con tres números, los números cuánticos: la distancia al núcleo (n), la medida de su momento angular (l) y un número que mide la orientación de la órbita del electrón en el espacio(m). En la figura se ilustra como afectan a la órbita los números l y m para un n fijado.
Así, en el Helio sus dos electrones tienen el estado (n,l,m)=(1,0,0), mientras que en el Litio, con tres electrones, no podemos tener el tercer electrón en el mismo estado (1,0,0), ha de ocupar el siguiente estado libre.
Posteriormente se añadió un cuarto número cuántico para describir la rotación del electrón alrededor de su propio eje, el denominado espín (s), con lo que el estado quedó definido por (n,l,m,s). De este modo, el principio de exclusión adoptó una forma más precisa: dos electrones de un átomo no pueden tener el mismo conjunto de números cuánticos (n,l,m,s). En esta formulación, el principio permitió avanzar en el conocimiento de la estructura electrónica de los átomos, en el fundamento de la valencia química y en la espectroscopia y el magnetismo.
¿Pero porqué solo afecta a los electrones de un núcleo? Imaginemos que dos átomos están “cerca” (como sucede cuando forman una molécula), ¿como sabe un electrón que ha de obedecer al principio de “su” átomo y no al del vecino? Lo que sucede en realidad es que en este caso de proximidad de dos átomos se formulan números cuánticos relativos al conjunto de átomos, que son diferentes al de un átomo aislado, y el principio de exclusión se aplica entonces a todos los electrones en conjunto.
Otra generalización posterior estableció que la exclusión afecta a todas las partículas elementales que pertenecen a la clase denominada fermiones, los cuales son los constituyentes básicos de la materia; no se aplica en cambio a la otra clase existente de partículas, los bosones, que actúan como portadoras de fuerzas (por ejemplo es un bosón el fotón, el componente cuántico de la luz).
Cuasifuerzas y antisimetria
El principio de exclusión junto con la repulsión eléctrica impide que los átomos se interpreneten, ya que cunado los números cuánticos están ocupados por electrones ya no podemos añadir ninguno más. Esto sugiere que está en juego alguna fuerza repulsiva.
Usando funciones de onda y probabilidades, sean dos partículas materiales A y B con funciones de onda u(A) y v(B) . Las probabilidades de encontrar A y B en las posiciones x(A) y x(B) vienen dadas por u²(A) y v²(B) respectivamente. Según las reglas usuales de las probabilidades, la probabilidad de encontrar A en x(A) y B en x(B) simultáneamente es el producto de probabilidades u²(A)·v²(B) siempre que A y B sean independientes. Entonces si consideramos A y B como un sistema único de dos partículas, su función de onda sería
Pero esta función conjunta de A y B no satisface el principio de exclusión, o sea que la naturaleza no se comporta así con las partículas materiales; hay que modificar la función para que adopte esta otra forma:
Si las partículas A y B fueran idénticas en el sentido de tener el mismo estado u(A) = v(B), es fácil ver que w(A,B) = 0 y por tanto la probabilidad de encontrar el sistema en cualquier posición sería cero. Esta es otra forma de enunciar el principio de exclusión. La función w(A,B) se dice que es antisimétrica debido a que si intercambiamos A y B obtenemos w(B,A) = - w(A,B).
Fijémonos en el detalle de que en la ecuación las partículas A y B se intercambian sus funciones u y v. Además, en cuanto a probabilidades, la fórmula implica que A y B no son independientes, hay una interacción entre A y B. Además, usando las expresiones de las funciones de onda en w(A,B) y realizando operaciones se llega a que es imposible (probabilidad = 0) que las partículas lleguen a juntarse, y tampoco pueden tener la misma velocidad. Así, dos partículas en principio libres se "evitan" entre sí, y el efecto parece que sea una fuerza de repulsión. Pero hay un detalle sutil: no podemos incorporar esa fuerza a la función de onda de la partícula, surge de la antisimetría impuesta por el principio de exclusión.
Podemos comparar el concepto con el de la fuerza de la gravedad en la teoría de la relatividad general: surge como consecuencia de la geometría del espacio-tiempo. Por esto las llamamos "cuasifuerzas". Tanto la cuántica como la gravedad, ¡se deducen de propiedades matemáticas!
La "no localidad"
Podríamos pensar que los efectos del principio de exclusión son locales, en el sentido de que tiene efecto sólo cuando las partículas están cercanas; han habido intentos de explicar este principio cuántico y los demás acudiendo a teorías de variables locales "ocultas", que explicarían todo en términos de interacción local (cercana) pero que no hemos podido detectar aún (ocultas).
Pero no es así: el físico John S. Bell enunció y demostró su teorema que viene a decir:
El teorema implica que debemos aceptar que hayan interacciones a distancias arbitrarias entre partículas cuánticas, y estas interacciones han de ser instantáneas. Para entender la implicación de esta afirmación, supongamos que dos partículas que forman un sistema con función de onda w(A,B) (técnicamente diremos que tienen entrelazamiento cuántico) empiezan a separarse una de otra a toda velocidad, y eventualmente llegan a estar separadas por kilómetros de distancia; a pesar de ello, siguen formando un sistema entrelazado, de tal manera que ciertas mediciones efectuadas en una de las partículas, ¡afectaran instantáneamente a la otra! Esto será así independientemente de la distancia que las separa. Este hecho fue confirmado por Alain Aspect en una serie de experimentos.
Conclusiones
En los cuatro posts de esta serie dedicada a entender la mecánica cuántica hemos expuesto con un mínimo de matemáticas los fundamentos de la teoría. El próximo post será "menos físico" y más "filośofico", en el sentido de intentar mostrar las implicaciones de toda la teoría de cara a nuestro conocimiento de la realidad física.
 |
| Paquete de ondas: hay oscilación apreciable sólo en una región Δx, fuera de ella es despreciable. |
 |
| Superposición de ondas |
Matemáticamente los paquetes de onda se forman por superposición de ondas distintas que interfieren entre sí. Físicamente se denominan estados puros a las ondas componentes que al combinarse forman los estados compuestos, representados por paquetes de ondas. Cada estado puro tiene asociada una función de onda cuántica, y el estado compuesto es la suma de funciones de onda.
Hay una relación entre estos estados y el proceso de medición: si en un sistema en estado puro se efectúa una medición, el sistema pasa a estar en un estado compuesto: la medición destruye el estado puro. Por ejemplo un electrón libre, antes de efectuar mediciones, está en un estado puro, con una función de onda "simple" que se extiende por todo el espacio; en el momento de medirlo le forzamos a comportarse como partícula, con lo cual se convierte en un paquete de ondas localizado que es una mezcla de estados puros.
De la mecánica clásica de Newton a la mecánica cuántica
La ecuación fundamental de la mecánica de Newton relaciona la masa m y la aceleración a de una partícula con la fuerza F que la impulsa, variable según la posición x:
donde hemos expresado la aceleración como la segunda derivada de la posición. Por otro lado la dinámica cuántica está determinada por la ecuación de Schrödinger que es
F(x) = m·a(x) = m·d²x/dt² ,
donde hemos expresado la aceleración como la segunda derivada de la posición. Por otro lado la dinámica cuántica está determinada por la ecuación de Schrödinger que es
Hφ = i·h·dφ/dt,
donde φ es la función de onda de la partícula, relacionada con la probabilidad de encontrarla en una cierta posición, H es el operador de Hamilton, relacionado con la energía de la partícula, y dφ/dt es la variación de φ con el tiempo. Con un poco de matemáticas que no detallaremos, esta ecuación se transforma en
F(X) = m·A(X) = m·d²X/dt²,
idéntica a la de Newton pero con los parámetros X, A que representan los valores medios de la posición x y la aceleración a. Esto tiene sentido pues trabajamos con probabilidades. Cuando lo aplicamos a un objeto grande, la onda tiene una posición definida y una probabilidad cercana al 100% de estar en esa posición, así que el valor medio coincide con el valor observado. De esta forma la mecánica clásica trabaja con valores medios muy estables y definidos, mientras que en la cuántica los valores oscilan según marcan las probabilidades dadas por la función de onda.
Evolución del paquete de ondas con el tiempo
Evolución del paquete de ondas con el tiempo
Decíamos que el operador H está relacionado con la energía; supongamos que ésta sea constante, o sea independiente del tiempo. Entonces la ecuación de Schrödinger que describe la evolución con el tiempo de la onda φ(x,t) al resolverla nos dice que, si el paquete de ondas está libre (no confinado), se irá expandiendo hasta ocupar todo el espacio, dejando de ser un paquete de ondas para convertirse en una onda libre. A este fenómeno se le llama difusión del paquete de ondas. En la práctica significa que, después de haber localizado una partícula con una medición, al pasar el tiempo la partícula vuelve a exhibir un comportamiento ondulatorio y le perdemos la pista: ya no podemos predecir su posición en el futuro, sólo la probabilidad de que esté en una posición.
 |
| Expansión de una función de onda libre con el tiempo t: inicialmente la probabilidad de encontrar la partícula está confinada a una región estrecha, pero la evolución con el tiempo predicha por la ecuación de Schrödinger va ampliando la región y finalmente ocupará todo el espacio. |
El principio de exclusión
 |
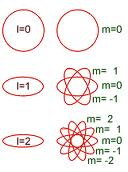| Números cuánticos |
Así, en el Helio sus dos electrones tienen el estado (n,l,m)=(1,0,0), mientras que en el Litio, con tres electrones, no podemos tener el tercer electrón en el mismo estado (1,0,0), ha de ocupar el siguiente estado libre.
Posteriormente se añadió un cuarto número cuántico para describir la rotación del electrón alrededor de su propio eje, el denominado espín (s), con lo que el estado quedó definido por (n,l,m,s). De este modo, el principio de exclusión adoptó una forma más precisa: dos electrones de un átomo no pueden tener el mismo conjunto de números cuánticos (n,l,m,s). En esta formulación, el principio permitió avanzar en el conocimiento de la estructura electrónica de los átomos, en el fundamento de la valencia química y en la espectroscopia y el magnetismo.
¿Pero porqué solo afecta a los electrones de un núcleo? Imaginemos que dos átomos están “cerca” (como sucede cuando forman una molécula), ¿como sabe un electrón que ha de obedecer al principio de “su” átomo y no al del vecino? Lo que sucede en realidad es que en este caso de proximidad de dos átomos se formulan números cuánticos relativos al conjunto de átomos, que son diferentes al de un átomo aislado, y el principio de exclusión se aplica entonces a todos los electrones en conjunto.
Otra generalización posterior estableció que la exclusión afecta a todas las partículas elementales que pertenecen a la clase denominada fermiones, los cuales son los constituyentes básicos de la materia; no se aplica en cambio a la otra clase existente de partículas, los bosones, que actúan como portadoras de fuerzas (por ejemplo es un bosón el fotón, el componente cuántico de la luz).
Cuasifuerzas y antisimetria
El principio de exclusión junto con la repulsión eléctrica impide que los átomos se interpreneten, ya que cunado los números cuánticos están ocupados por electrones ya no podemos añadir ninguno más. Esto sugiere que está en juego alguna fuerza repulsiva.
Usando funciones de onda y probabilidades, sean dos partículas materiales A y B con funciones de onda u(A) y v(B) . Las probabilidades de encontrar A y B en las posiciones x(A) y x(B) vienen dadas por u²(A) y v²(B) respectivamente. Según las reglas usuales de las probabilidades, la probabilidad de encontrar A en x(A) y B en x(B) simultáneamente es el producto de probabilidades u²(A)·v²(B) siempre que A y B sean independientes. Entonces si consideramos A y B como un sistema único de dos partículas, su función de onda sería
w(A, B) = u(A)·v(B)
Pero esta función conjunta de A y B no satisface el principio de exclusión, o sea que la naturaleza no se comporta así con las partículas materiales; hay que modificar la función para que adopte esta otra forma:
w(A,B) = u(A)·v(B) - u(B)·v(A)
Si las partículas A y B fueran idénticas en el sentido de tener el mismo estado u(A) = v(B), es fácil ver que w(A,B) = 0 y por tanto la probabilidad de encontrar el sistema en cualquier posición sería cero. Esta es otra forma de enunciar el principio de exclusión. La función w(A,B) se dice que es antisimétrica debido a que si intercambiamos A y B obtenemos w(B,A) = - w(A,B).
 |
| Probabilidades de los estados de un sistema de dos partículas que obedece al principio de exclusión: en la diagonal estan los estados idénticos con probabilidad nula, y en los extremos los estados totalmente distintos con mayor probabilidad. |
Podemos comparar el concepto con el de la fuerza de la gravedad en la teoría de la relatividad general: surge como consecuencia de la geometría del espacio-tiempo. Por esto las llamamos "cuasifuerzas". Tanto la cuántica como la gravedad, ¡se deducen de propiedades matemáticas!
La "no localidad"
Podríamos pensar que los efectos del principio de exclusión son locales, en el sentido de que tiene efecto sólo cuando las partículas están cercanas; han habido intentos de explicar este principio cuántico y los demás acudiendo a teorías de variables locales "ocultas", que explicarían todo en términos de interacción local (cercana) pero que no hemos podido detectar aún (ocultas).
Pero no es así: el físico John S. Bell enunció y demostró su teorema que viene a decir:
"Ninguna teoría física de variables ocultas locales puede reproducir todas las predicciones de la mecánica cuántica"
El teorema implica que debemos aceptar que hayan interacciones a distancias arbitrarias entre partículas cuánticas, y estas interacciones han de ser instantáneas. Para entender la implicación de esta afirmación, supongamos que dos partículas que forman un sistema con función de onda w(A,B) (técnicamente diremos que tienen entrelazamiento cuántico) empiezan a separarse una de otra a toda velocidad, y eventualmente llegan a estar separadas por kilómetros de distancia; a pesar de ello, siguen formando un sistema entrelazado, de tal manera que ciertas mediciones efectuadas en una de las partículas, ¡afectaran instantáneamente a la otra! Esto será así independientemente de la distancia que las separa. Este hecho fue confirmado por Alain Aspect en una serie de experimentos.
Conclusiones
En los cuatro posts de esta serie dedicada a entender la mecánica cuántica hemos expuesto con un mínimo de matemáticas los fundamentos de la teoría. El próximo post será "menos físico" y más "filośofico", en el sentido de intentar mostrar las implicaciones de toda la teoría de cara a nuestro conocimiento de la realidad física.
No hay comentarios:
Publicar un comentario
Los comentarios por favor que sean sobre el tema del artículo, y siempre para completar, o para preguntar. No se admitiran comentarios que no cumplan estas premisas ni por supuesto que sean ofensivos bajo ningun concepto.