"Procura, pues, desviar tu corazón de lo visible y traspasarlo a lo invisible..."
Tomás de Kempis (siglo XV)
En la serie de posts "Entendiendo la mecánica cuántica" (partes I, II, III y IV) hemos repasado los hechos básicos de la teoría cuántica. En este post pretendo tratar, brevemente, las implicaciones filosóficas de la teoría, fundamentalmente respecto a la noción científica de realidad.
Realismo físico y objetividad
La postura respecto a la realidad de la mayoría de científicos consiste en postular que la naturaleza posee una realidad objetiva independiente de nuestras percepciones o de nuestros instrumentos, de modo que el objeto de la ciencia es describir esa realidad objetiva. Por otra parte las teorías platónicas sostienen que la realidad nunca podrá entenderse por ninguna teoría basada en la experiencia.
La postura científica expuesta usa el concepto de objetividad: es objetiva toda afirmación que sea válida para cualquier observador. Esta definición tiene alguna ambigüedad, ya que recurre a un observador, en principio un ser humano, para poder definir la realidad objetiva; esto pone al observador en una posición privilegiada como el validador de la realidad, y además obliga a distinguir entre observadores válidos y no válidos, por ejemplo exigiendo que tengan sentido común para entender lo observado. Por ello llamaremos objetividad débil a esta definición.
El principio de objetividad fuerte postula que toda afirmación respecto a la naturaleza debería ser independiente de los observadores, en el sentido de que no hará ninguna referencia a ellos, no los necesita. Ésta es la postura mayoritaria en la ciencia: las leyes de la ciencia describen la naturaleza en términos de objetividad fuerte.
La realidad fragmentada de la ciencia clásica
Es también habitual en la ciencia tener la visión analítica del Universo en la cual éste se descompone en un número inmenso de elementos simples, que pueden estudiarse por separado. Cada elemento ocupa en cada instante de tiempo un lugar definido en el espacio, y puede interactuar con los otros elementos de forma predecible. Es una visión atomista que llamaré postulado de la fragmentabilidad. Por ejemplo la teoría de campos electromagnéticos de Maxwell postula que un campo tiene unos valores en el tiempo y en el espacio que pueden cambiarse "aquí y ahora" sin afectar a los valores del campo en posiciones suficientemente lejanas, y por tanto sostiene la fragmentabilidad de la realidad.
Es interesante señalar que la fragmentación que propone la ciencia analítica probablemente esté relacionada con el funcionamiento básico de nuestra mente, que trabaja fundamentalmente así, descomponiendo la realidad en objetos independientes. Escribí sobre esto en un post anterior: ¿La mente está orientada a objetos?
Entonces, podríamos aventurar que la ciencia ha sido como es, con una visión fragmentada de la realidad, debido a que nuestra mente trabaja de forma natural de esa forma; esto es importante, pues la realidad en sí no tiene porqué ser fragmentable, con lo cual la ciencia nos estaría ofreciendo una visión distorsionada de la realidad. Probablemente es esto lo que sucedió hasta el descubrimiento de la Física cuántica, que nos forzó a revisar nuestro concepto, firmemente establecido hasta ese momento, de un Universo compuesto por fragmentos relativamente independientes.
Es interesante señalar que la fragmentación que propone la ciencia analítica probablemente esté relacionada con el funcionamiento básico de nuestra mente, que trabaja fundamentalmente así, descomponiendo la realidad en objetos independientes. Escribí sobre esto en un post anterior: ¿La mente está orientada a objetos?
Entonces, podríamos aventurar que la ciencia ha sido como es, con una visión fragmentada de la realidad, debido a que nuestra mente trabaja de forma natural de esa forma; esto es importante, pues la realidad en sí no tiene porqué ser fragmentable, con lo cual la ciencia nos estaría ofreciendo una visión distorsionada de la realidad. Probablemente es esto lo que sucedió hasta el descubrimiento de la Física cuántica, que nos forzó a revisar nuestro concepto, firmemente establecido hasta ese momento, de un Universo compuesto por fragmentos relativamente independientes.
Los límites de la fragmentación de la materia: Leibniz y Kant
El razonamiento filosófico ya hace milenios que trabajaba con el concepto de fragmentación de la realidad, de sus posibilidades y límites. Por razonamientos puramente filosóficos, Demócrito ya postuló los atomos, que consideró indivisibles e indestructibles, como componentes básicos de la materia, y desde el siglo XIX que sabemos que estuvo acertado en general, ¡2300 años más tarde! El proceso por el que llegó a tal conclusión en parte seguro que fue empírico, en el sentido de que observó las incesantes transformaciones de la materia, y como se formaban nuevas sustancias a partir de combinaciones de otras, en un proceso contínuo. Una forma eficaz de explicarlo era postulando los átomos como constituyentes de todo, y toda materia estaría formada por las virtualmente infinitas combinaciones posibles de esos átomos.
Claro que, con los átomos, también persistía un problema filosófico: ¿qué los hacía indestructibles? ¿Por qué tenían que serlo? ¿De qué estaban constituidos para ser eternos e indestructibles?
El razonamiento filosófico ya hace milenios que trabajaba con el concepto de fragmentación de la realidad, de sus posibilidades y límites. Por razonamientos puramente filosóficos, Demócrito ya postuló los atomos, que consideró indivisibles e indestructibles, como componentes básicos de la materia, y desde el siglo XIX que sabemos que estuvo acertado en general, ¡2300 años más tarde! El proceso por el que llegó a tal conclusión en parte seguro que fue empírico, en el sentido de que observó las incesantes transformaciones de la materia, y como se formaban nuevas sustancias a partir de combinaciones de otras, en un proceso contínuo. Una forma eficaz de explicarlo era postulando los átomos como constituyentes de todo, y toda materia estaría formada por las virtualmente infinitas combinaciones posibles de esos átomos.
Claro que, con los átomos, también persistía un problema filosófico: ¿qué los hacía indestructibles? ¿Por qué tenían que serlo? ¿De qué estaban constituidos para ser eternos e indestructibles?
En la teoría filosófica conocida por la monadología de Leibniz (para ver el razonamiento completo teneis por ejemplo el post substancias simples y compuestas) se postula que todo es compuesto o simple (indivisible), y por un razonamiento lógico se infiere que "toda substancia simple ha de se inmaterial y por tanto espiritual". En cambio Kant usando el mismo postulado concluye que incluso las partes simples también deben ocupar un espacio, y siendo el espacio siempre divisible, lo simple será divisible, y por reducción al absurdo, concluye que no existen las sustancias simples indivisibles.
La función de onda cuántica, ¿podría ser la "substancia simple" filosófica?
A principios de siglo XX lo indivisible creíamos que era el átomo, pero posteriormente los aceleradores de partículas han sido capaces de romper cualquier elemento constituyente de la materia, átomos, núcleos, partículas, todo. Así que parecía que era Kant quien tenía razón: no hay substancias simples indivisibles. ¿Queda algo indivisible? Lo que nos queda como indivisible es algo sutil, como no podía ser de otra manera: las funciones de onda cuánticas (ver si es necesario Entendiendo la mecánica cuántica III), que son a mi parecer los candidatos actuales a "substancias" simples, no materiales, indivisibles, espirituales según Leibnitz. Por combinación de funciones de onda se forman estados compuestos, los cuales a su vez se combinan infinidad de veces para formar los objetos de nuestro mundo macroscópico habitual.
Además, las funciones de onda invalidan la argumentación de Kant, según el cual las partes simples deben ocupar un espacio y por tanto serán divisibles, pero con las funciones de onda cuánticas es justamente al contrario: su caracter es no-local, ocupa todo el espacio, y por ello no puede ser dividido. En cambio los estados compuestos por superposición de ondas, como más complejos son, más localizados en el espacio están; en el límite macroscópico estan muy localizados.
Se puede objetar que la función de onda es meramente un instrumento matemático sin existencia real y por tanto no puede ser considerada como el componente básico de la materia. Ésta es una confusión típica: la función de onda efectivamente tiene una expresión matemática que usamos para los cálculos, pero a la vez es la conceptualización de algo real que está allí, con lo que se puede interactuar en el laboratorio, y de hecho el nacimiento de toda la teoría cuántica fue experimental, no teórico ni filosófico. Se encontró que la naturaleza del mundo subatómico era no fragmentada.
A principios de siglo XX lo indivisible creíamos que era el átomo, pero posteriormente los aceleradores de partículas han sido capaces de romper cualquier elemento constituyente de la materia, átomos, núcleos, partículas, todo. Así que parecía que era Kant quien tenía razón: no hay substancias simples indivisibles. ¿Queda algo indivisible? Lo que nos queda como indivisible es algo sutil, como no podía ser de otra manera: las funciones de onda cuánticas (ver si es necesario Entendiendo la mecánica cuántica III), que son a mi parecer los candidatos actuales a "substancias" simples, no materiales, indivisibles, espirituales según Leibnitz. Por combinación de funciones de onda se forman estados compuestos, los cuales a su vez se combinan infinidad de veces para formar los objetos de nuestro mundo macroscópico habitual.
Además, las funciones de onda invalidan la argumentación de Kant, según el cual las partes simples deben ocupar un espacio y por tanto serán divisibles, pero con las funciones de onda cuánticas es justamente al contrario: su caracter es no-local, ocupa todo el espacio, y por ello no puede ser dividido. En cambio los estados compuestos por superposición de ondas, como más complejos son, más localizados en el espacio están; en el límite macroscópico estan muy localizados.
Se puede objetar que la función de onda es meramente un instrumento matemático sin existencia real y por tanto no puede ser considerada como el componente básico de la materia. Ésta es una confusión típica: la función de onda efectivamente tiene una expresión matemática que usamos para los cálculos, pero a la vez es la conceptualización de algo real que está allí, con lo que se puede interactuar en el laboratorio, y de hecho el nacimiento de toda la teoría cuántica fue experimental, no teórico ni filosófico. Se encontró que la naturaleza del mundo subatómico era no fragmentada.
Los límites de nuestro conocimiento de la realidad
Tenemos que toda la ciencia, excepto la Física cuántica, usa el postulado de la fragmentabilidad, y supone tambien cierto el principio de objetividad fuerte. El mundo cuántico no respeta ninguno de estos postulados: la no localidad implica la no fragmentabilidad, y además pierde sentido la noción de observador independiente de lo observado, pues la función de onda cuántica del objeto se superpone con la del observador, son no separables. Es por estas razones que se suele decir que no podemos entender realmente la Física cuántica. La forma "estándar" de afrontar esta "extrañeza" del mundo subatómico es la conocida por interpretación de Copenhague que nos dice que renunciemos a tener más conocimiento de la realidad más allá de la probabilidades que permite calcular la matemática de la mecánica cuántica. Han habido numerosas objeciones y contrapropuestas a esta concepción, entre las cuales destacaré la de David Bohm (en este blog he tratado de su teoría en diversas ocasiones).
Realismo no físico y teoría cuántica de campos
Recapitulando, tenemos que la ciencia ha conseguido analizar y dividir la materia hasta un grado impresionante (recordemos que un átomo tiene un tamaño típico de 10⁻⁸ cm, y que su núcleo es 10.000 veces menor), pero en ese proceso de división y análisis de los fragmentos resultantes, ¡ha llegado a perder los fragmentos! En efecto, las partículas muestran propiedades ondulatorias, lo cual implica que estan dispersadas por el espacio, ilocalizables, y lo que es peor, con posibilidad de interactuar instantáneamente desde lugares arbitrariamente alejados, algo más bien inconcebible según la ciencia clásica.
En un campo cuántico localmente se producen partículas, más o menos estables, que interactúan con la radiación y con elpropio campo.¿Qué son estas partículas realmente? Recordemos que son los constituyentes de toda la materia que nos rodea (y que nos forma). Pero por otro lado tenemos que, cuando estan aisladas, se deslocalizan, y sólo adquieren una posición cuando interactuamos con ellas en el proceso llamado medición. Dicho sea de paso, también hay teorías que relacionan este proceso de localización con la conciencia del sujeto que realiza la medición. La medición proporciona magnitudes, pero debido al principio de indeterminación, no podemos obtener el conocimiento simultáneo de ciertos pares de magnitudes, como la posición y la velocidad. Entonces cuando interactuamos con la partícula, sólo podemos obtener un conocimiento limitado de ella, de forma que para el experimentador tal partícula se reduce a algunas magnitudes denominadas observables, que estan relacionadas con propiedades, pero ¿propiedades de qué?
En los anteriores posts hemos hablado de la mecánica cuántica a un nivel básico; modernamente se ha desarrollado la teoría, y se han formulado variantes especializadas. La más general es la teoría cuántica de campos. En esta teoría, bien fundamentada en la actualidad, una partícula no es más que una propiedad de una realidad inmaterial, un modo de vibración de un "algo" subyacente, informe e ilimitado, que matemáticamente representamos con un campo: una regla de correspondencia que asigna unos valores a cada punto del espacio-tiempo. Vemos así que la investigación, lejos de resolver la pérdida de la objetividad y la localidad, al contrario, disuelve aún más los componentes de la materia considerándolos meramente propiedades observables de una realidad inmaterial que se extiende por todo el espacio. El gran reto de la Física del siglo XXI consiste en conseguir que esta teoría abarque a la gravedad y la relatividad general; es opinión generalizada que la gravedad debe ser cuantizada, y por tanto también el espacio-tiempo.
En un campo cuántico localmente se producen partículas, más o menos estables, que interactúan con la radiación y con elpropio campo.¿Qué son estas partículas realmente? Recordemos que son los constituyentes de toda la materia que nos rodea (y que nos forma). Pero por otro lado tenemos que, cuando estan aisladas, se deslocalizan, y sólo adquieren una posición cuando interactuamos con ellas en el proceso llamado medición. Dicho sea de paso, también hay teorías que relacionan este proceso de localización con la conciencia del sujeto que realiza la medición. La medición proporciona magnitudes, pero debido al principio de indeterminación, no podemos obtener el conocimiento simultáneo de ciertos pares de magnitudes, como la posición y la velocidad. Entonces cuando interactuamos con la partícula, sólo podemos obtener un conocimiento limitado de ella, de forma que para el experimentador tal partícula se reduce a algunas magnitudes denominadas observables, que estan relacionadas con propiedades, pero ¿propiedades de qué?
 |
| Campo cuántico: partículas = modos locales |
Ser
 |
| Recreación artística del ser ocupando todo |
Bibliografía
- Bernard d'Espagnat: En busca de lo real. Alianza Universidad.
- Henry Margenau: La naturaleza de la realidad física. Tecnos.

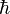 es la
es la 





 , un
, un